Vektorgeometrie: Abstand Punkt/Ebene (1)

Vorbereiten des 3D-Modells

Auf der Grundplatte ein Koordinatensystem festlegen (blau = ^ x 1 , grün = ^ x 2 )

Markieren Sie einen beliebigen Punkt P im Raum, z.B. so:

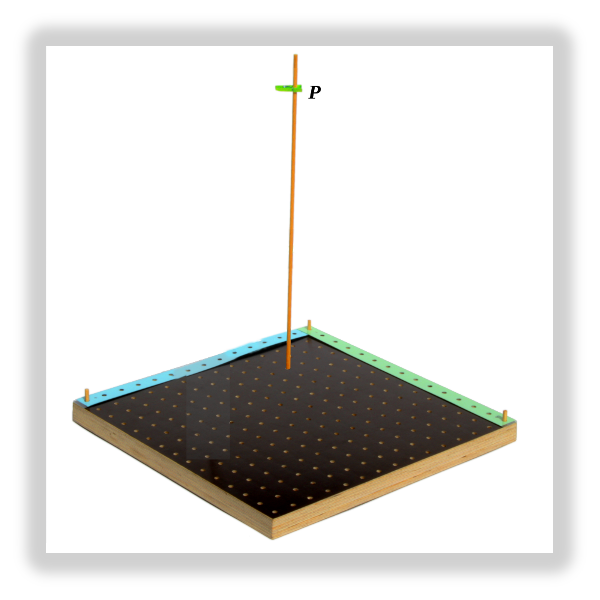
Forschungsauftrag (1)

  1. Bestimmen Sie experimentell einen Punkt Q in der x1 x2 - Ebene, so dass der Abstand zwischen P und Q so minimal wie möglich ist. Begründen Sie schriftlich ihr Vorgehen.
    Lösung 1
  2. Beschreiben Sie die Lage der x1 x2 - Ebene zur Geraden durch P und Q .
    Lösung 2

Umbau des 3D-Modells

Fügen Sie in Ihr Modell die Ebene E mit E :  x → = 0 0 4 + t 1 0 0 + s 0 2 -1 mit Hilfe eines Blatt Papiers ein und verschieben Sie P an die Koordinaten 5 9 7 .

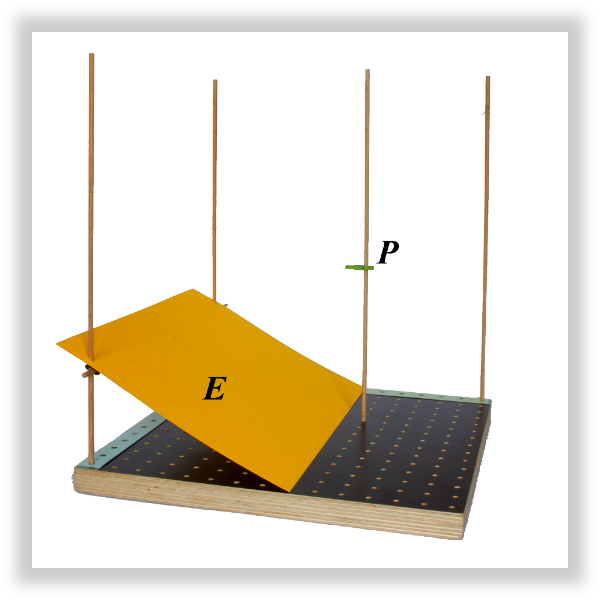
Forschungsauftrag (2)

  1. Ermitteln Sie mit Hilfe der Erkenntnisse aus dem Forschungsauftrag (1) die Koordinaten eines Punktes Q , so dass der Abstand zwischen P und Q minimal ist und Q in der Ebene E liegt.
    Lösung 3
  2. Bestimmen Sie die Gleichung einer Geraden g , die durch P und Q verläuft.
    Tipp 1
    Lösung 4
  3. Q ist der Schnittpunkt der Geraden g mit der Ebene E . Bestimmen Sie rechnerisch die Koordinaten von Q .
    Tipp 2
    Lösung 5
  4. Berechnen Sie die Länge von PQ → . Dies ist der (kürzeste) Abstand zwischen P und der Ebene E .
    Lösung 6

Abstand leicht gemacht, bei Geraden

g ist eine Gerade mit g :  x → = 5 -2 6 + t 1/3 2/3 2/3 , deren Stützvektor auf den Punkt P 5 -2 6 zeigt. Für t=6 liefert die Geradengleichung den Ortsvektor zum Punkt Q .

  1. Bestimmen Sie die Koordinaten von Q .
    Lösung 7
  2. Berechnen Sie den Abstand zwischen P und Q .
    Lösung 8
  3. Begründen Sie, den sichtbaren Zusammenhang zwischen t und dem Abstand der Punkte P und Q .
    Lösung 9

h ist eine Gerade mit h :  x → = 2 4 -1 + t 8 0 6 , deren Stützvektor auf den Punkt A 2 4 -1 zeigt. Für t=0,5 liefert die Geradengleichung den Ortsvektor zum Punkt B .

  1. Bestimmen Sie die Koordinaten von B .
    Lösung 10
  2. Berechnen Sie den Abstand zwischen A und B .
    Lösung 11
  3. Warum besteht der Zusammenhang zwischen t und dem Abstand der Punkte in diesem Fall nicht? Begründen Sie.
    Lösung 12
  4. Geben Sie eine Gleichung für h an, bei der sich der Abstand zwischen A und eines weiteren Punktes direkt von t ablesen lässt (so wie bei der Geraden g )
    Lösung 13

Umbau des 3D-Modells

Fügen Sie in Ihr Modell die Ebene E :  x → - 0 0 6 ⋅ 0 3 4 = 0 mit Hilfe eines Blatt Papiers ein und verschieben Sie P an die Koordinaten 8 10 11 .

Fügen Sie eine Gerade g in das Modell ein, so dass g durch P geht und senkrecht auf E steht.

Markieren Sie den Schnittpunkt von g und E mit Q .

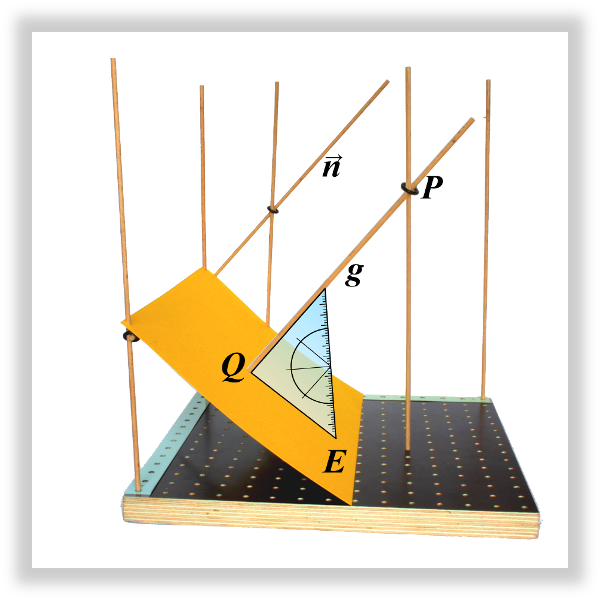
Optimierung des Lösungswegs

  1. Eine Gleichung zu g ist g :  x → = 8 10 11 + t ⋅ n → . Bestimmen Sie n → , so dass n → ein Einheitsvektor ist.
    Was ist ein Einheitsvektor?
    Lösung 14
  2. Begründen Sie, dass En mit En :  x → - 0 0 6 ⋅ n → = 0 und E die selben Ebenen beschreiben.
    Lösung 15

    Definition:
    Ist der Normalenvektor in einer Ebenengleichung in Normalform ein Einheitsvektor, so heißt die Ebenengleichung Hess'sche Normalform.

  3. Messen Sie im 3D-Modell den Abstand zwischen P und Q .
    Lösung 16
  4. Bestimmen Sie aus dem gemessenen Abstand und ohne Rechnung einen Wert für t , so dass q → = 8 10 11 + t ⋅ n → .
    Lösung 17
  5. Um die Koordinaten von Q zu berechnen, wird der Term 8 10 11 + t ⋅ n → in die Ebenengleichung eingesetzt und nach t afgelöst: 8 10 11 + t ⋅ n → - 0 0 6 ⋅ n → = 0
    Beschreiben Sie in Worten, welche Umformungen mit jedem Schritt gemacht werden:
    8 10 11 + t ⋅ n → - 0 0 6 ⋅ n → = 0 ↓
    Schritt 1
    ⇔ 8 10 11 - 0 0 6 + t ⋅ n → ⋅ n → = 0 ↓
    Schritt 2
    ⇔ 8 10 11 - 0 0 6 ⋅ n → + t ⋅ n → 2 = 0 ↓

    Lösung 18
  6. Zeigen Sie, dass 8 10 11 - 0 0 6 ⋅ n → + t ⋅ n → 2 = 8 10 11 - 0 0 6 ⋅ n → + t ist und damit 8 10 11 - 0 0 6 ⋅ n → = - t , bzw. 8 10 11 - 0 0 6 ⋅ n → = t .
    Tipp 3
    Lösung 19
  7. Der Abstand von P und E lässt sich somit mit d = t = p → - s → ⋅ n → berechnen. Woher kommen die Vektoren p → , s → und n → ?
    Lösung 20